A canonical labeling technique by Brendan McKay and isomorphism testing of deterministic finite automata

A deterministic finite automaton (DFA) $M$ is a 5-tuple, $(Q, \Sigma, \delta, q_0, F)$ , consisting of

a finite set of states $Q$
a finite set of input symbols $\Sigma$
a (partial) transition function $\delta:Q\times \Sigma \to Q$
an initial state $q_0\in Q$
a set of accept states $F \subset Q$

An isomorphism between two DFAs $M = (Q, \Sigma, \delta, q_0, F)$ and $M' = (Q', \Sigma, \delta', q'_0, F')$ is a bijection $p:Q\to Q'$ such that $\delta'(\cdot,s) = p \circ \delta(\cdot,s) \circ p^{-1} \forall s\in\Sigma$ , $q'_0 = p(q_0)$ and $F' = p(F)$ .

Isomorphism of DFA is GI complete

Without further restrictions, the problem of testing whether two DFAs $M$ and $M'$ are isomorphic is as difficult as testing whether two graphs $G$ and $G'$ are isomorphic, i.e. the problem is GI complete. A simple construction shows that the problem of testing whether two digraphs $G$ and $G'$ are isomorphic reduces to DFA isomorphism testing.

For a digraph $G=(V,E)$ , construct the DFA $M_G=(Q_G, \Sigma, \delta_G, q_0, F)$ with $Q_G:=V \sqcup E \sqcup \{*\}$ , $\Sigma := \{0,1\}$ , $q_0:=*$ , $F:=\{ \}$ and $\delta_G$ defined for $e\in E$ by $\delta_G(e,0)=\text{tail}(e)$ , $\delta_G(e,1)=\text{head}(e)$ and for $v\in V\sqcup \{*\}$ by $\delta_G(v,0)=\delta_G(v,1)=*$ .
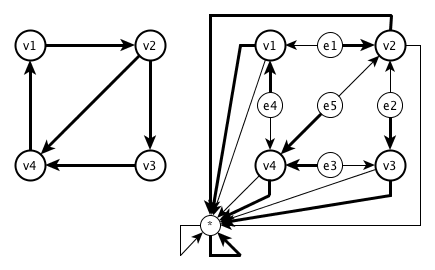
Digraph and corresponding DFA
Obviously, the digraphs $G$ and $G'$ are isomorphic iff the DFAs $M_G$ and $M_{G'}$ are isomorphic.

A canonical labeling technique

A reasonable restriction is to require that every state in $Q$ is reachable from $q_0$ . Let $\Sigma:=\{s_1,\ldots,s_d\}$ . Then a unique labeling $\ell(q_0)$ of $Q$ can be produced by a breadth first search of $M$ starting at $q_0$ as follows: You have a queue (first-in, first-out store), initially containing only $q_0$ . Repeatedly do this: remove the state at the head of the queue, say $x$ , then push into the queue (at the tail) those of $\delta(x,s_1),\ldots,\delta(x,s_d)$ (in that order) which have never previously been put into the queue. Since every state is reachable from $q_0$ , every state is put into the queue eventually. Stop when that has happened and define $\ell(q_0)$ to be the order in which states were put into the queue. Since this labeling is independent of any ordering or labeling of $Q$ , it fixes the only bijection between $Q$ and $Q'$ that can possibly lead to an isomorphism between $M$ and $M'$ . It is easy then to check whether they are actually isomorphic.

Attributing that algorithm to Brendan McKay would be misleading, because it is so obvious. For example J.-E. Pin described the same algorithm (using depth first search instead of breadth first search) earlier, as an answer to a question about finding an isomorphism between finite automata.

Brendan McKay’s canonical labeling technique

The context in which Brendan McKay described his canonical labeling technique was actually slightly more complicated, because there was no distinguished state $q_0$ , and the state space of the automaton wasn’t required to be weakly connected. But instead, $\delta(\cdot,s)$ was injective for all $s\in S$ . If we drop the requirement that $\delta(\cdot,s)$ is a total function and allow it to be partial, then we end up exactly with the reversible deterministic finite automata, described earlier on this blog. Brendan McKay’s technique generalizes effortlessly to this setting, as does the original context (where group actions are replaced by inverse semigroup actions).

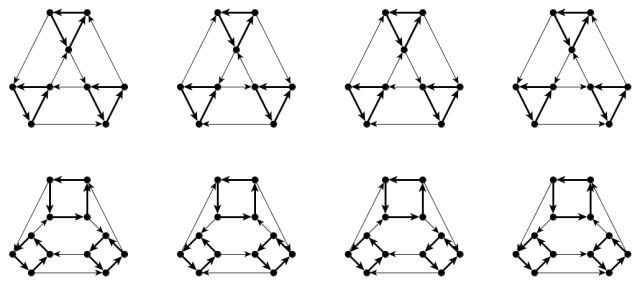
Above are some colored digraphs corresponding to reversible deterministic finite automata (the initial state $q_0$ and the final states $F$ are ignored). We continue to describe the canonical labeling technique in terms of deterministic finite automata. For each state $q\in Q$ , we can produce a unique labeling $\ell(q)$ (of the weakly connected component containing $q$ ) by a breadth first search of $M$ starting at $q$ as above, expect when we remove the state $x$ from the head of the queue, (instead of $\delta(x,s_1),\ldots,\delta(x,s_d)$ ) we have to push into the queue (at the tail) those of $\delta(x,s_1),\delta^{-1}(x,s_1),\ldots,\delta(x,s_d),\delta^{-1}(x,s_d)$ (in that order) which are defined and have never previously been put into the queue.

But how can we create a canonical labeling of $M$ from the unique labelings $\ell(q)$ ? Just take (one of) the lexicographically smallest labelings of each block, and sort the block lexicographically based on those labelings. The lexicographical order in this context is defined by encoding a labeled block in some reasonable (unique) way as a string, and comparing those strings lexicographically. It’s a good idea to modify this lexicographical order to first compare the lengths of the strings, but this is already an optimization, and there are more possible optimizations, as described in Brendan’s answer. These optimizations are the context of the following remark at the end of his answer:

The graph is actually a deterministic finite automaton (at most one edge of each colour leaves each vertex). There could be faster isomorphism algorithms out there for DFAs, though I’m dubious that anything would work faster in practice than a well-tuned implementation of the method I described.

This remark was actually the main motivation of this blog post, i.e. to investigate the relation of Brendan’s technique to isomorphism testing for DFAs. If there were really faster isomorphism algorithms out there for DFAs, then either they would not be applicable to the problem which Brendan had solved there (if they rely on reachability from $q_0$ ), or they would also solve GI itself in polynomial time (which is highly unlikely).

Conclusions?

The truth is I have been yak shaving again, even so I explicitly told vzn that I didn’t want to get too involved with GI. How did it happen? Fahad Mortuza (aka Jim) asked me for help refuting his attempts to solve GI in quasipolynomial time. (This is completely unrelated to the recent breakthrough by László Babai, except maybe that he triggered some people to spend time on GI again.) While working with him, I realized that permutation group isomorphism might be more difficult than group isomorphism, and asked some questions to get a better feeling for the relation of permutation group isomorphism to GI. The idea to consider the case where the group is fixed came from reading an introduction to category theory, because those morphisms of left $M$ -sets felt like cheating (or oversimplifying) to me. So I guessed that this case should be easy to solve, if I would only understand how Brendan McKay handles automorphisms of graphs efficiently. Then Brendan McKay himself explained his technique (for this case) and I discovered the interesting connection to inverse semigroups and finite automata, so I decided I had to write a blog post on this. Now I have written this post, just to avoid having another item on my ToDo list which never gets done.

4 Responses to A canonical labeling technique by Brendan McKay and isomorphism testing of deterministic finite automata

vznvzn says:

January 26, 2016 at 10:48 pm

💡 a new idea thinking about this. could FSM theory be leveraged against GI somehow? in particular it seems like (building on all this) DFA minimization might somehow be a natural way to test for GI. hmmm…..

- gentzen says:
  
  February 7, 2016 at 12:57 pm
  
  Well, the first step of DFA minimization is to throw away all states not reachable by the initial state. For the DFA constructed above, only the initial state $q_0:=*$ will be left. So we can’t use DFA minimization to test for GI.
  
  But DFA minimization can be used to highlight an interesting point. We could ask why GI is important, and how it relates to equivalence (or identity) testing for computational structures like DFA or straight line programs. Even so these tasks look more complicated than GI, the fastest known algorithm for GI takes quasi-polynomial time, while equivalence testing of DFA can be done in quasi-linear time, and identity testing of straight line programs can be done randomized in polynomial time. But the last step for equivalence testing of DFA after DFA minimization is indeed isomorphism testing for the minimized DFAs. And because every state is reachable from the initial state for these minimized DFAs, we see that these DFAs can be tested for isomorphism in linear time, by the technique described above.
  
vznvzn says:

February 9, 2016 at 2:01 am

think there is some broad theory that could be devised here, mused on this many years ago & its cool this post reminds me of it. youve made the basic observation that canonical graph labellings create basically DFA objects. my rough idea from many years ago is that some canonical graph labellings seem to lead to a natural algorithm for isomorphism based on DFA minimization. my vague ideas for the algorithm were something like:
a. canonically label the two graphs using some scheme X.
b. do DFA minimization on each graph. if there is a mismatch in vertex degree distribution, graphs are not isomorphic.
c. then compute if the DFAs are equivalent using intersection emptiness/ complement testing. (DFA A in DFA B iff A in B and B in A). if they are not equal, conclude graphs are not isomorphic.
d. conclude graphs are isomorphic.
then the natural question is, what are labelling schemes X that lead to this being a reliable isomorphism algorithm? in the sense of low false positives and negatives? do such schemes exist? is there a scheme that “always” works without false positives/negatives?

Pingback: Learning category theory: a necessary evil? | Gentzen translated